113k views asked in Class XII Maths by nikita74 (1,017 points) Find the general solution of y 2 dx (x 2 xyy 2 )dy = 0 differential equations 95k views asked in Class XII Maths by rahul152 (2,8 points) Find the general solution of (x2y 3) dy/dx = y differential equationsNCERT solutions for Class 12 Maths Chapter 9 Differential Equations Pages 413 414 Q 1 Page 413 For the differential equations find the general solution `dy/dx 2y = sin x` VIEW SOLUTION Q 2 Page 413 For the differential equations find the general solution `dy/dx
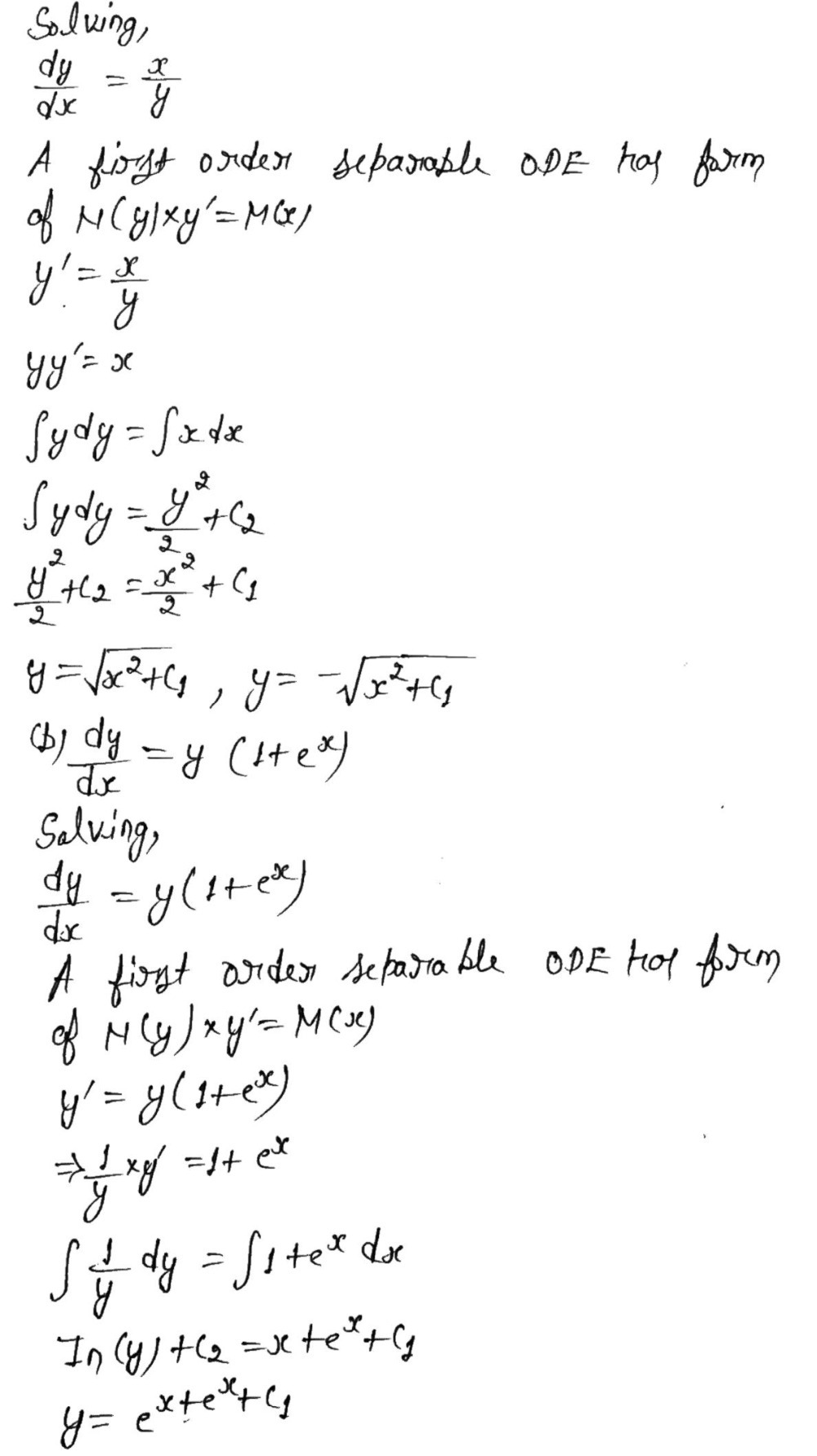
Exercises 2 Find The General Solution Of The Foll Gauthmath
Find the general solution of the differential equation (x-y)dy/dx=x+2y
Find the general solution of the differential equation (x-y)dy/dx=x+2y- x^2y^2=c dy/{dx}=x/y ydy=xdx by exploiting the notation (separation) int ydy=int xdx further exploiting the notation 1/2y^2=1/2x^2d y^2=x^22d x^2y^2=2d x^2y^2=c where c=2d Depending on whether c is positive, negative or zero you get a hyperbola open to the xaxis, open to the y=axis, or a pair of straight lines through the originFind the general solution for the differential equation dy/dx 2y=18e^x ;
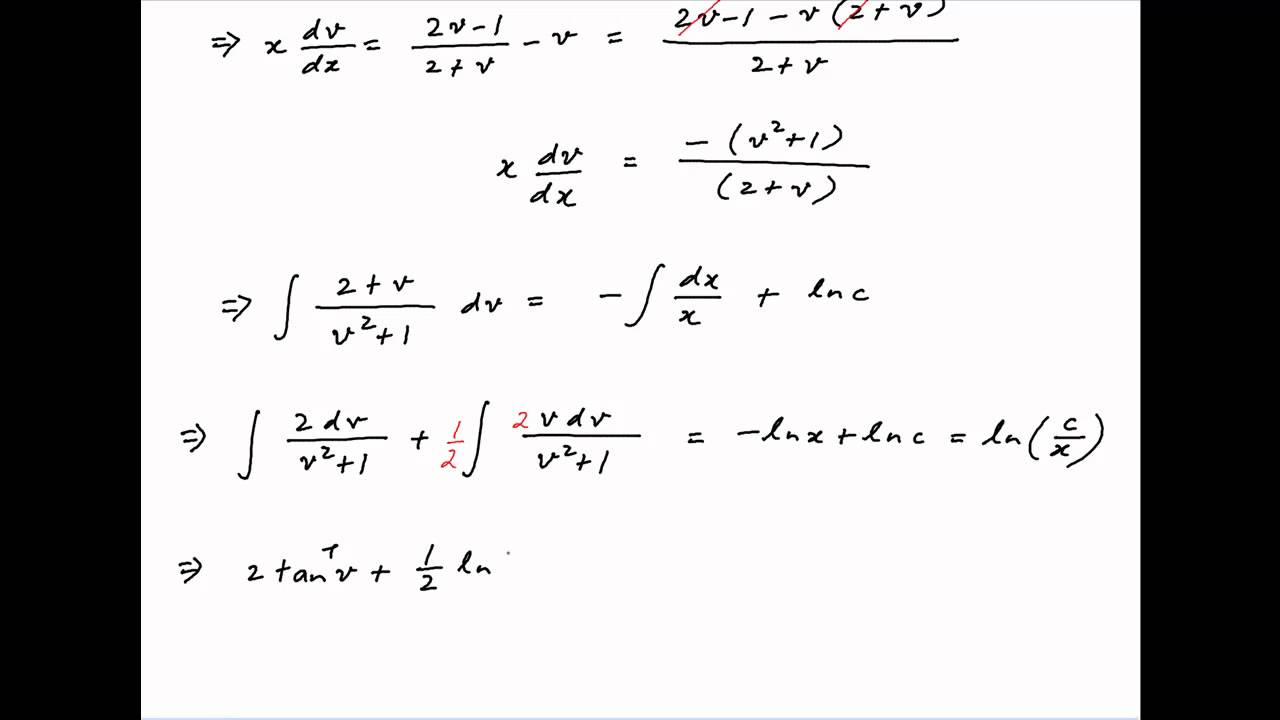



Solve The Differential Equation Dy Dx 2y X 2x Y Youtube
Find general solution to x (dy/dx) 2y = 4x^2 Divide through by x so (dy/dx) 2 (y/x) = 4x Now multiply through by the intergrating factor e^ ( (2/x) dx) = e^ (2ln (x)) = x^2 so you get (x^2) (dy/dx) 2xy = 4 (x^3) Now integrate the entire equation and you get y (x^2) = (4 (x^3))dx = (x^4) c Divide through by (x^2) to get the solve (cosx tany cos (xy))dx (sin x sec 2 ycos (xy))dy=0 differentialequation derivatives asked in CALCULUS by linda ScholarWe cannot separate the variables, so we hope that it is linear It is linear if we can get it in the form then we can solve it by multiplying by the
Answer to Obtain the general solution of {dy} / {dx} = (3 y) x^2 using the variable separable method By signing up, you'll get thousands ofSeparabledifferentialequationcalculator x\frac{dy}{dx}=y^{2} en Related Symbolab blog postsAd by Best Gadget Advice 25 insanely
Dy dx = 3x 4y y 2x SOLUTION Divide numerator and denominator by x, and let v= y x (the equation is a homogeneous equation), therefore y= xvand y0= xv0 v Although we don't need to solve the DE, we should go ahead and separate the variables xv0 v= 3 4v v 2) xv0= 3 4v v(v 2) v 2 = 3 2v v2 v 2) v 2 3 2v v2 dv= 1 x dx 1A differential equation of the form dy dx P (x)y =Q(x)yn d y d x P ( x) y = Q ( x) y n is called Bernoulli's equation It can be reduced to a linear differential equation by substituting u= y1Separable equations can be written in the form dy/dx=f (x)g (y) See how we analyze various differential equations to see if they are separable Finding general solutions using separation of variables Separable equations introduction Addressing treating differentials algebraically Separable differential equations




X 2y 3 Xy Dy Dx



Differential Equation Help D2jsp Topic
The differential equation corresponding to the equation y 2 = a ( b − x 2) where a, b are constants is J & K CET 13 7 If x y = A s i n x B c o s x is the solution of the differential equation x d 2 y d x 2 − 5 a d y d x x y = 0 then the value of a is equal to KEAM 13 8Share It On Facebook Twitter Email 1 Answer 0 votes answered by AbhishekAnand (870k points) selected by Vikash Kumar Best answer Given that, ← PrevGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



1



How To Solve Math X 3y 3 Xy Dx Dy Math Using Differential Equations Quora
Dy dx P(x)y = Q(x)yn, where n 6= 1 (the equation is thus nonlinear) To find the solution, change the dependent variable from y to z, where z = y1−n This gives a differential equation in x and z that is linear, and can be solved using the integrating factor method Note Dividing the above standard form by yn gives 1 yn dy dx P(x)y1−nThe general solution of the differential equation dy / dx = x y 1 / 2x 2y 1 is 1) loge 3x 3y 2 3x 6y = C 2) loge 3x 3y 2 3x 6y = C 3) loge 3x 3y 2 3x – 6y = C 4) loge 3x 3y 2 3x – 6y = C Solution (4) loge 3x 3y 2 3x – 6y = C b e g i n a r r a y l t e x t G i v e n f r a c d y d xWhat is the General solution for exact differential equation cosx tany cos(xy) dx sinx sec^2ycos(xy) dy=0 ?



How To You Find The General Solution Of Dy Dx X Y Socratic




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora
Find the general solution of (x 2y 3)dy/dx = y differential equations; Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeStep 2 Integrate both sides of the equation ∫dy = ∫2x dx → &int1 dy = &int2x dx → y = x 2 C Example problem #2 Find the general solution for the differential equation dy ⁄ dx = x 2 – 3 Step 1 Use algebra to get the equation into a more familiar form for integration dy ⁄ dx = x 2 – 3→ dy = x 2 – 3 dx Step 2 Integrate both sides of the equation



Find The General Solution Of Y2dx X2 Xy Y2 Dy 0 Studyrankersonline



Solve 2 Y 3 Xy Dy Dx 0 Given That Y 1 2 Studyrankersonline
Thus, the general solution is given implicitly by the equation x2y2 x3 y4 = C 1636 Verify that the DE (1 ye xy )dx (2yxe xy )dy = 0 is exact, and find its general Show that the differential equation dy/dx = y^2/(xy x^2) is homogeneous and also solve it asked in Mathematics by monuk ( 680k points) differential equationsSimple and best practice solution for (xy)dx(xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it
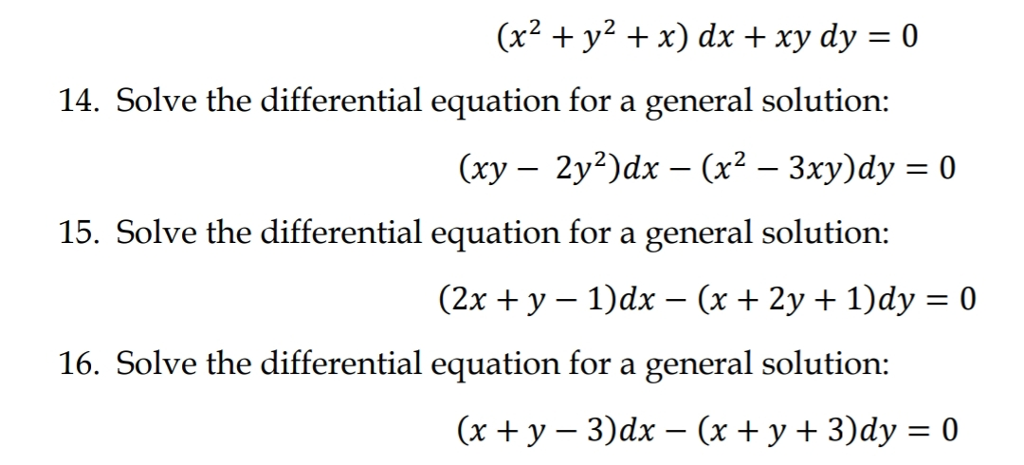



X2 Y2 X Dx Xy Dy 0 14 Solve The Differential Chegg Com
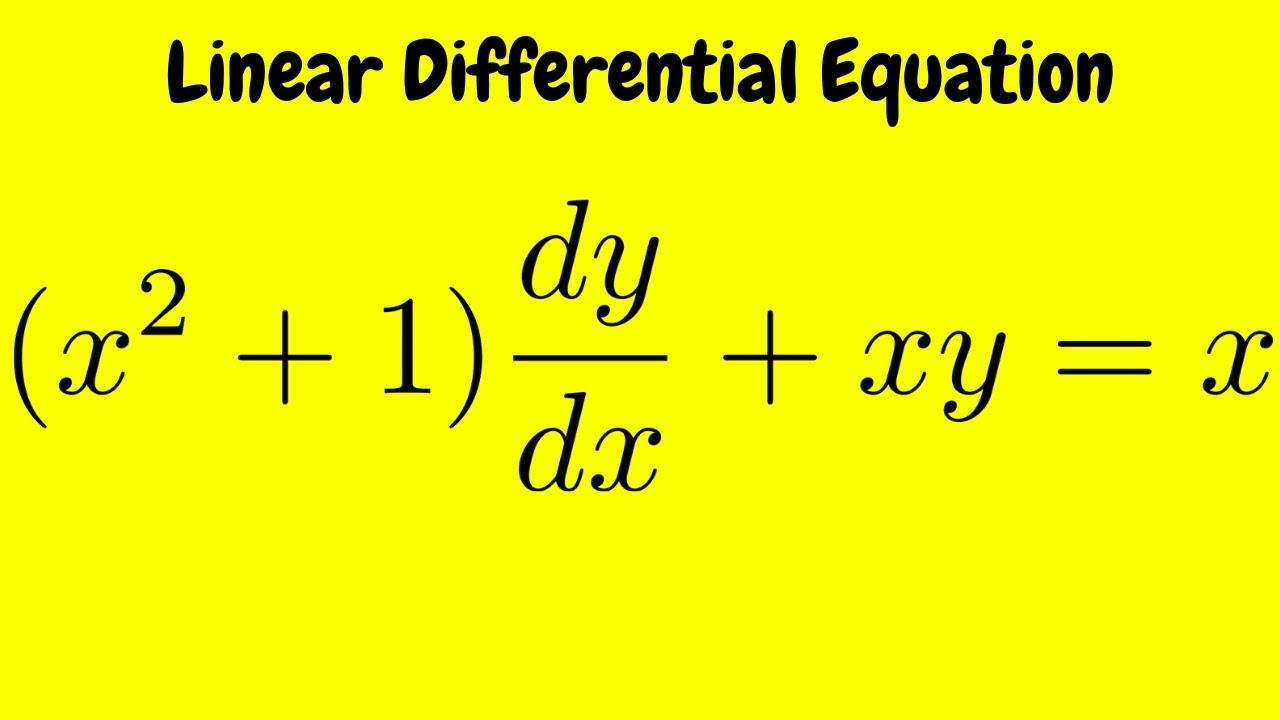



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube
Solve ordinary differential equations (ODE) stepbystep Derivatives First Derivative Specify Method (new) Chain Rule Product Rule Quotient Rule Sum/Diff Rule Second DerivativeSlope At Any Point (x, y) Of A Parabola y = Cx 2 That slope is the derivative dy / dx of y = Cx 2 at the point (x, y) Elimination Of The Constant C The constant C is eliminated in the calculation of the derivative dy / dx of y = Cx 2, and dy / dx is expressed in terms of both x and y This is because an orthogonal curve would be orthogonal2 3 х 2 and 4 1 and 5 O 13i none of these Solve the initial value problem х 3 2 х 4 x(0) = 0, y(0) = 1 Ox(t) = etel y(t) = e 2e O x(1) = sin(t) y(t) = cos(1) X(t




Ex 9 6 11 Find General Solution Y Dx X Y2 Dy 0




Hw 2 5 Solutions Differential Equations Equations
1 Find the general solution of the following system of equations dx dt = xy, dy dt = 3x− y Solution We can rearrange this system to obtain one secondorder differential equation Differentiatethefirst equationwith respect tottoobtain d2x dt2 = dx dt dy dt Substituting for dy dt from the second equation then gives d2x dt2 = dx dtExample 1 Solve d 2 ydx 2 − 3 dydx 2y = e 3x 1 Find the general solution of d 2 ydx 2 − 3 dydx 2y = 0 The characteristic equation is r 2 − 3r 2 = 0 Factor (r − 1)(r − 2) = 0 r = 1 or 2 So the general solution of the differential equation is y = Ae x Be 2x So in this case the fundamental solutions and their derivatives are Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Misc 11 Find Particular Solution X Y Dx Dy Dx Dy




Ordinary Differential Equations
Question Find the general solution of this linear differential equation (x^4 2y)dxxdy=0 Answer by Edwin McCravy () ( Show Source ) You can put this solution on YOUR website!P(x)dx and so dim(W)=1 (Remark Solutions of nonhomogeneous or nonlinear equations may not form a vector space ) 10 Solve the linear rst order linear IVP y0 ytanx= sin2x;Simple and best practice solution for (x2y)(dxdy)=dxdy equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it




How To Solve The Differential Equation X 2 Y 2 Dx Xydy 0 Quora



Solve The Differential Equation Dy Dx 2y X 2x Y Youtube
2 Problem 3 Give the general solution to y0 y2 sin(x) = 0 First write in standard form dy dx = −y2 sin(x) ⇒ − 1 y2 dy = sin(x)dx Before going any further, notice that we have divided by y, so we need to say that this is value as long as y(x) 6= 0 In fact, we see that the function y(x) = 0 IS a possible solutionY(0) = 1 Recall For y0 p(x)y = r(x), the left hand side becomes exact if we multiply by (x) = exp(R p(x)dx))We get d dx ( (x)y) = (x)r(x)Integrating, generalThe differential equation of the form is given as d y d x = y x Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of the
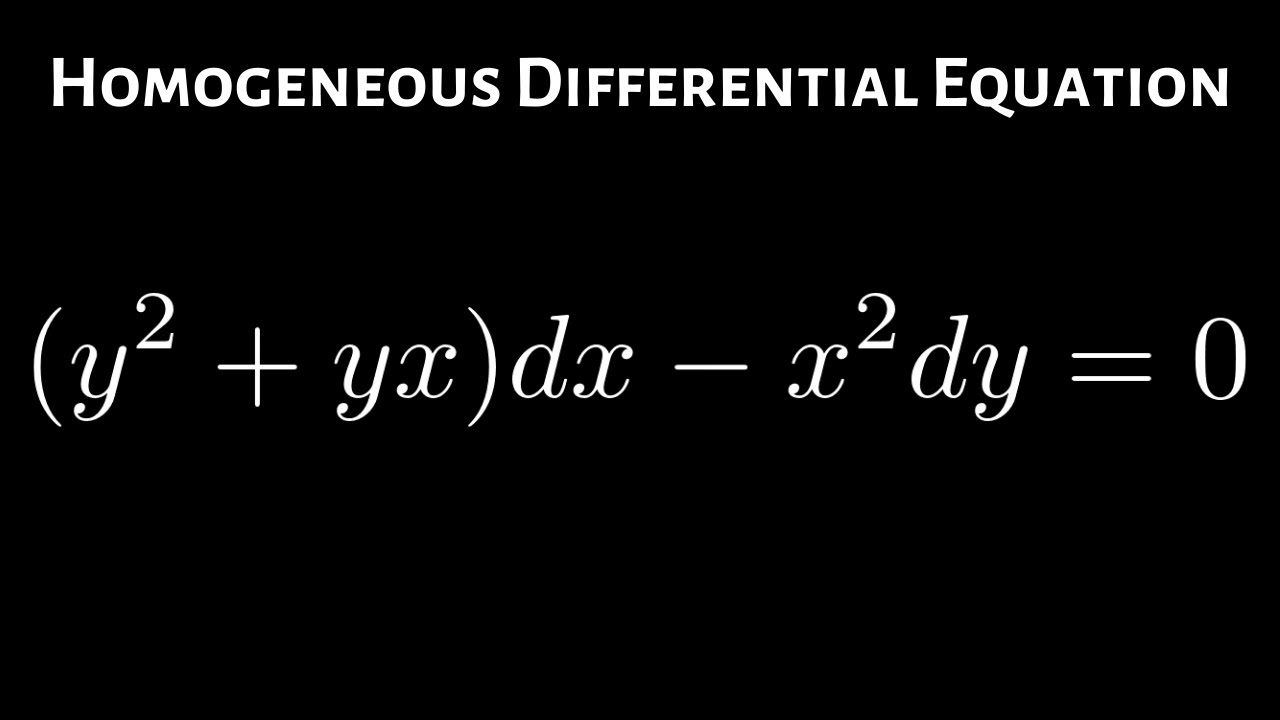



Homogeneous Differential Equation Y 2 Yx Dx X 2dy 0 Youtube




Solve Xy Cos Xy Sin Xy Dx X 2cos Xy Dy 0
Solution We have, x = dy dx 2y = x2 ⇒ dy dx 2 xy = x The above equation is a linear differential equation in y ∴ IF = e ∫ 2 xdx = e2logx = x2 Hence, required solution will be y x2 = ∫ x x2dx C1 ⇒ yx2 = x4 4 C1 ⇒ yx2 = x4 4C1 4Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more4 y(8x9y)dx 2x(x3y)dy = 0 substitute y=vx, v is a function of x substitute back v=y/x isolate y Answer 6 2(2y 2 5xy2y4)dxx(2x2y1)dy=0 let y be the dependent variable Divide by dx substitute dy/dx with y' Rewrite in the form of an exact differential equation if the conditions are met, then The general solution is Ψ(x,y)=C




1 First Order Ode S 18 03 Exercises 1a Introduction Separation Of Variables




Solve Xy Dy Dx X 2 Y 2
First we find solution to the corresponding homogeneous equation math\qquad y'' 2y' y = 0/math by setting up and finding roots of characteristicExample 1 Solve the differential equation dy / dx 2 x y = x Solution to Example 1 Comparing the given differential equation with the general first order differential equation, we have P(x) = 2 x and Q(x) = x Let us now find the integrating factor u(x) u(x) = e ò P(x) dx = e ò2 x dx = e x 2 We now substitute u(x)= e x 2 and Q(x) = x in the equation u(x) y = ò u(x) Q(x) dx to obtainSolved Examples Example 1 Solve the LDE = dy/dx = 1/(1x 3) – 3x 2 /(1 x 2)y Solution The above mentioned equation can be rewritten as dy/dx 3x 2 /(1 x 2) y = 1/(1x 3) Comparing it with dy/dx Py = O, we get P = 3x 2 /1x 3 Q= 1/1 x 3 Let's figure out the integrating factor(IF) which is \( e^{\int Pdx} \) ⇒IF = \( e^{\int \frac {3x^2}{1 x^3}} dx = e^{ln (1 x^3)} \)




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com




First Order Differential Equations Ppt Download
Click here👆to get an answer to your question ️ The general solution of (2x y 1) dx (2y x 1) dy = 0 isA first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx What is the differential equation of the family of parabolas having their vertices at the origin and their foci on the xaxis A 2x dy – y dx = 0 B x dy y dx = 0 C 2y dx – x dy = 0 D dy/dx – x




Differential Equations Separation Of Variables Ppt Download




Dy Dx X 2y X X 2y X Mathematics Topperlearning Com 84onrx44
Find the general solution (2x y)dx (x 2y)dy = 0 O x2 y2 xy = C O x2 y2 2xy = C O x2 y2 x y = C none of these What are the eigenvalues for this system? Ex 96, 1 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑑𝑦/𝑑𝑥2𝑦=𝑠𝑖𝑛𝑥 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q 𝑑𝑦/𝑑𝑥2𝑦=sin𝑥 Step 2 Find P and Q Comparing (1) with 𝑑𝑦/𝑑𝑥 Py = Q ∴ P = 2 and Q = sin x (1) Step 3 FindClick here👆to get an answer to your question ️ Solution of the differential equation y(2xy e^x) dx e^x dy = 0 is



What Is The Exact Differential Equation Of X Y Dx X Y 1 Dy 0 Quora




Example 21 Find General Solution Ydx X 2y2 Dy 0
Differential Equation Calculator The calculator will find the solution of the given ODE firstorder, secondorder, nthorder, separable, linear, exact, Bernoulli, homogeneous, or inhomogeneous Initial conditions are also supported Your input solve $$$ y ' \left (x \right) = x^ {2} $$$




1 9 Fghbhj Equations Function Mathematics



Www Tau Ac Il Levant Ode Solution 6 Pdf




The General Solution Of Differential Equation Dy Dx X Y X Y




Engineering Mathematics Notes



Find The General Solution Of The Differential Equation X Y Dy Dx X 2y Sarthaks Econnect Largest Online Education Community



Find The Particular Solution Of The Following Differential Equation Xy Dy Dx X 2 Y 2 Y 1 When X 1 Sarthaks Econnect Largest Online Education Community




I Determine Whether Each Of The Following Differe Gauthmath




The General Solution Of Dy Dx Xy 2 X Y Is In Chegg Com




Dy Dx X 2 Y 2 Novocom Top




Dy Dx X 2y 3 Xy 1 Novocom Top




Engineering Mathematics Notes




Compute The General Solution Of Each Of The Following Chegg Com




Example 15 Show X Y Dy Dx X 2y Is Homogeneous Solve



Exercises 2 Find The General Solution Of The Foll Gauthmath




Consider The Differential Equation Xy 2 Bx 2y Dx Chegg Com




Show That The Given Differential Equation Is Homogeneous And Solve Each Of Them X 2 Dy Dx X 2 2y 2 Xy Mathematics Shaalaa Com
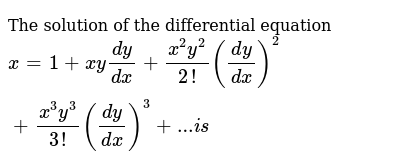



The Solution Of The Differential Equation X 1 X Y Dy Dx X 2




Exact Equations Example 3 Video Khan Academy



Show That The Differential Equation X Y Dy Dx X 2y Is Homogeneous And Solve It Sarthaks Econnect Largest Online Education Community



Solve Dy Dx X 2y 3 Xy 1 Sarthaks Econnect Largest Online Education Community




How To Solve 3xy Y 2 Dx X 2 Xy Dy 0 Also I Wish To Knw When To Use Y Vx Or X Vy Mathematics Topperlearning Com H9faf2xx




Solution Of Y Xy 1 Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange



Solve The Differential Equation Xy 2 X Dx X 2y Y Dy 0 Sarthaks Econnect Largest Online Education Community
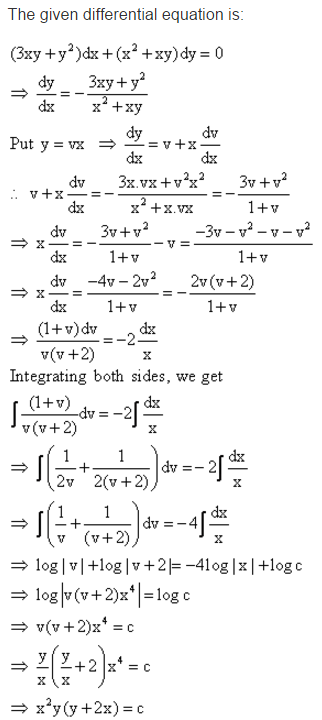



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633



3




Engineering Mathematics Notes



What Is The Solution To The Differential Equation Dy Dx 2x Y 1 4x 2y 1 Quora



1




X 2y Xy Y 0 Novocom Top




Exact Differential Equations




Dy Dx X 2 Y 2 Novocom Top




The Solution Of The Equation Dy Dx X 3y 2 Xy Is A X 2y 2y 1 C
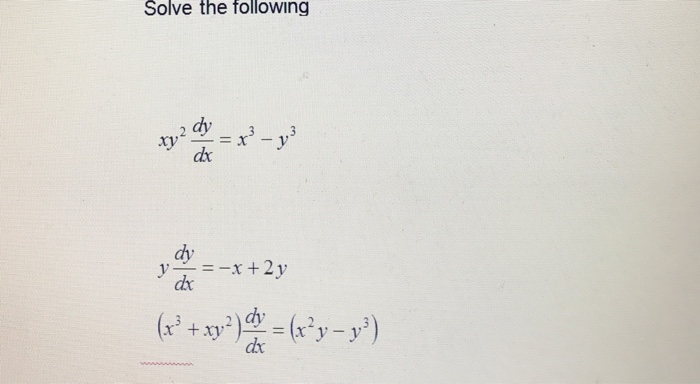



Solve The Following Xy 2 Dy Dx X 3 Y 3 Y Dy Dx Chegg Com




Find The General Solution Of The Following Chegg Com



Show That The Differential Equation X Y Dy Dx X 2y Is Homogeneous And Solve It Sarthaks Econnect Largest Online Education Community




Solve The Following Differential Equations I Y 2 D X Left X Y X 2 Right D Y 0 Ii X 2 Y D X Left X 3 Y 3 Right D Y 0 Iii Frac D Y D X Tan Left Frac Y X Right Frac Y X Iii Frac D Y D X Frac X 2 Y 2 X Y 0 Iv




Solve Each Differential Equation Dy Dx X 2y 2 Chegg Com




The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given Youtube




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com




Solve Xdy Dx X 2 Xy Y 2 X With Y 1 1 Find Chegg Com




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution




Solving Differential Equation Dy Dx X 2 Y 2 Xy X 2 If Y Ux Youtube



How To Find The General Solution Of Dy Dx 2y X Y Quora



Exercises 2 Find The General Solution Of The Foll Gauthmath



Solve The Following Differential Equation 1 X 2 Y 2 X 2y 2 Xy Dy Dx 0 Sarthaks Econnect Largest Online Education Community




Engineering Mathematics Notes
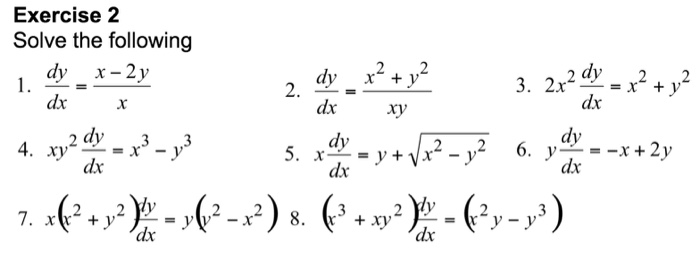



Solve The Following Dy Dx X 2y X Dy Dx X 2 Chegg Com




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download




X 2y Xy Y 0 Novocom Top




Engineering Mathematics Notes




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy




Ex 9 5 3 Show Homogeneous X Y Dx X Y Dx 0




A Curve Satisfies The Differential Equation Dy Dx X 1 Xy 2



Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community




Example 9 Find General Solution Of Dy Dx X 1 2 Y Examples




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution




Engineering Mathematics Notes




For What Value Of N Is Following A Homogeneous Differential Equation
.png)



Find Particular Solution Of The De X Y Dy Dx X 2y Given That When X 1 Y 0 Please Give The Solution Quickly Maths Differential Equations Meritnation Com




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Solution Solve The Linear Equation Dy Dx Y X X 2



Solve X Y Dx Dy Dx Dy Studyrankersonline




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2 Y Given That Y 0 When X 1 Brainly In



Solve X2 Dy Dx X2 Xy Y2 Studyrankersonline




Differential Equations Separation Of Variables Ppt Download




Ex 9 5 11 Find Particular Solution X Y Dy X Y Dx 0




Find Differential Equation Of 3xy Y 2 Dx X 2 Xy Dy Brainly In




Dy Dx X 2 Y 2 Novocom Top
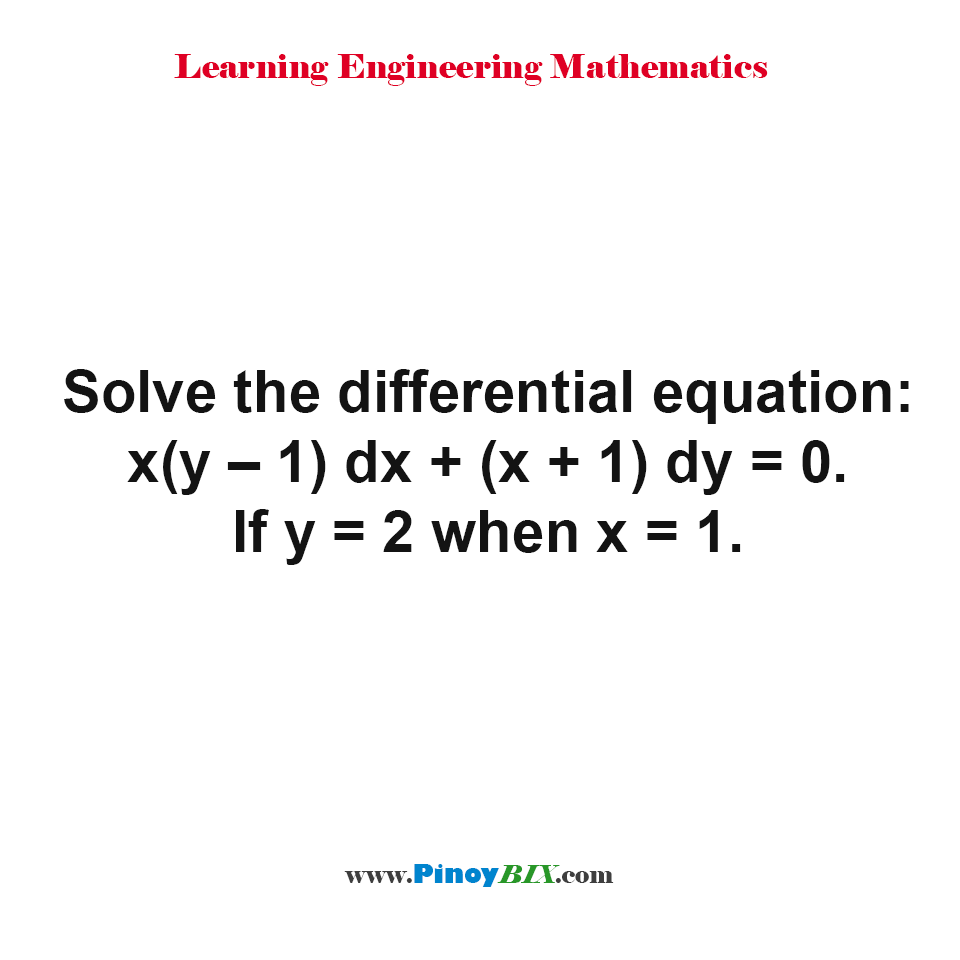



Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1



How To Solve For The General Solution Of The Following Differential Equation X 2 Y 2 1 Dx X X 2y Dy 0 Using An Integrating Factor Quora




A X Dy Dx 2y X Y Dy Dx



Find The Particular Solution Of The Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 For X 1 Y 1 Sarthaks Econnect Largest Online Education Community



Q Tbn And9gctmzre3xsgguvydb6zseicrc3f0floyled1xpcrvxjrg02gz44g Usqp Cau




Differential Equations Separation Of Variables Ppt Download



What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora




Answered 62 Chapter 2 First Order Differential Bartleby




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If




Solving The Bernoulli Differential Equation X 2 Dy Dx Y 2 Xy Youtube



0 件のコメント:
コメントを投稿